د ساده هارمونيکي حرکت تعريف

د ټال وهلو او يا زانگو حالت د يو کوچني تر څيړنې لاندې ونيسئ. وبه وينئ چې د ټال ټلئ وهل، په ډيره منظمه توگه په مســاوي وختونو کې خپله تگ او راتگ کوي. هر هغه حرکت چې پخپله په منظمه توگه تکراریږي. پيريود يک )تناوبي( يا هارمونيک حرکت نومیږي. يا په بل عبارت، هغه حرکت چې د ساين او يا کوســاين د گراف په وســيله ښــودل کیږي، ســاده هارمونيکي حرکت بلل کیږي.

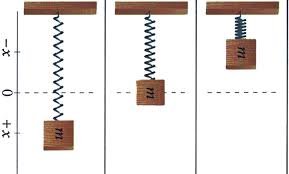
هــر کلــه چې وزنه په فنر پورې کلکيږي، نو فنر مخ ښــکته حرکت کوي، خو کله چې فنر اوږدیږي، په دې حالت کې د فنر لخوا يوه قوه ظاهریږي، چې د فنر قوه بلل کيږي. دغه قوه د هوک د قانون په ذريعه پـدې ډول وړانــدې کیږي.    .Fs =−k⋅x په دې رابطه کې k د فنرثابــت  او xد فنرهغه اوږدوالي دي چې د وزن له ځړولو وروسته د فنر په اوږدوالى کې مينځ ته راځي. هر کله چې د وزن مساوي قوه يعنې (mg ) د فنر په اوږدو پورته خواته موجه شــي، جســم يا وزن د تعادل په حالت کې غوره کوي. د شکل مطابق، کله چې وزن د L موقعيت ته پورته کیږي، په دې حالت کې د فنر لخوا عامله قوه پر وزن باندې صفر کیږي، کله چې هغه ازادانه پرې ښــودل شــي، نو مخ ښکته تعجيل اخلي او سرعت يا چټکتيا يې ورو ورو زياتیږي، ترڅو چې وزن بیرته د فنر د قوې د اغېزې لاندې راځي او ورو ورو بيرته د جســم يا وزن ســرعت کمیږي. د فنر د قوې او وزن د قوې د تعادل په حالت کې، ســرعت صفر او په نتيجه کې تعجيل هم فر کیږي. په بل عبارت نتيجوي عامله قوه پر وزن باندې سره انډول کیږي. د وزن د ښکته تــگ پــه وخــت کې دوزن قوه دفنرله قوې څخه زياته وي اوکله چــې وزن دفنر دقوې دتاثير لاندې مخ پورته حرکت کوي، نو په دې حالت کې د فنر لخوا عامله قوه د وزن له قوې څخه زياته ده. جســم د ترلاسه شوې قوې تر تاثير لاندې پورته خواته حرکت کوي، تر هغه وخته چې بيا قوې سره مساوي او د جسم سرعت صفر شي.

د وزن د D په موقعيت کې.  v=o دي. په  دغه حالت کې حرکي  انرژي کامًلا په پوتانشــيل انرژي اوړي او حرکي انرژي صفر کیږي. وزنه د عطالت د قوې لاندې بيا حرکت کوي. په دې ترتيب په مساوي وختونو کې د هغې وزن حرکت چې فنر پورې تړل شــوى دي تکراریږي. نو ځکه د غه حرکت ته ســاده هارمونيکي حرکت ويل کییي. اوس راځئ چې د ساده هارمونيکي حرکت لپاره يو بل تعريف پيداکړو. که چیرې په تير شوي فعاليت کــې اهتــزازي حرکت يو ځــل بيا وڅيړو، او که چیرې پــه دغه حرکت کې گړنديتوب ته ځير شــو، نو څرگنده به شــي، چې تعجيل هميشــه يوې نقطې ته موجه دي، د هغه قيمت د تعادل له نقطې څخه د بيځايه کیدو په فاصلې پورې متناســبه ده. له دغه ځاى څخه نتيجه اخلو چې هر متحرک جســم چې د حرکت په وخت پورتن9 تعجيلي خصوصيت ولري، ساده اهتزازي حرکت دي.